$ A-B $は、$(-1,1)$上に対称三角分布を持ちます。平均が0で、分散が$ \ frac {1} {6} $です。
$ | A-B | $の分布は$ \ text {beta}(1,2)$です。平均$ \ frac {1} {3} $と分散$ \ frac {1} {18} $があります。
ベータ確率変数の合計の分布は$ n = 2 $で知られています。 ( 1を参照)。
編集:
実際、この特定のベータ版は非常に単純なので、積分を実行できます。理由はわかりません。以前にそれを試してみませんでした。 $ Y_i = | A_i-B_i | $とします。 $ Z = Y_1 + Y_2 $の密度を計算でき、そこから$ 1- \ frac {1} {2} \ sum_ {i = 1} ^ 2 | A_i-B_i | $の分布を見つけることができます。
(畳み込み積分の)単純な直接積分により、
$ f_Z(z)= \ begin {cases} \ frac {2} {3} z \、(z ^ 2 -6z + 6)& \ mbox {for} 0<z \ leq 1 \\\ frac {2} {3}(2-z)^ 3 & \ mbox {for} 1<z \ leq 2 \\ 0 & \ mbox {elsewhere }。 \ end {cases} $
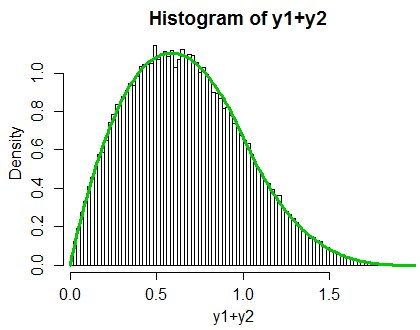
この場合、$ H_2 = 1-Z / 2 $の密度は、その密度の線形再スケーリングにすぎません。
[これは非常に急速に扱いにくくなります。私がこれを正しく行った場合、4つの$ Y_i $の合計はそれぞれ7次多項式で構成される4つの部分を持ち、8つはそれぞれ15次の多項式で構成される8つの部分を持ちます。優れた数式処理システムが手元にあれば、確かに計算できますが、有益なとは思えません。]
-
中程度の$ n $の場合、この比較的単純なケースでさえ代数的には知られていないと思いますが、数値的に、かなり簡単に畳み込みを行うことができます。
大きな$ n $の場合は可能です。中心極限定理を利用します。 $ 1- \ frac {1} {n} \ sum_ {i = 1} ^ n | A_i-B_i | $の平均と分散は単純です。エラーがなければ、$ \ frac {2です。 } {3} $および$ \ frac {1} {18n} $。
$ n = 8 $の場合はそれほど正確ではありませんが、$ n = 20 $の場合、正規近似はかなり良好です。
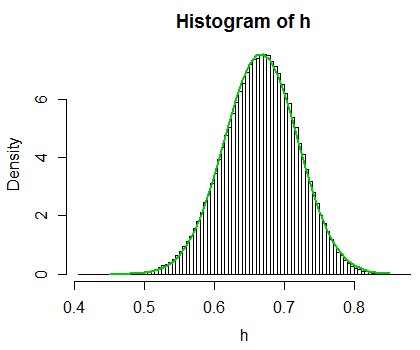
= ==
編集:
畳み込みを数値的に行うことができると言うとき、正確にはどういう意味ですか?正確には何を畳み込みますか?
$ Y_i = | A_i-B_i | $とすると、$ H = 1- \ frac {1} {n} \ sum_ {i = 1} ^ n Y_i $となります。
簡単な線形再スケーリングとは別に、$ Y_i $の合計の分布が必要です。
ここで畳み込みが発生します。 $ W + Z $の密度は、 PDFの畳み込みです。
もちろん、実際には、畳み込み積分は行いません。通常の統計的アプローチは、MGFまたはより一般的には特性関数を使用することですが、符号の問題(ここでも些細なこと)を除けば、CFは単なるフーリエ変換です(MGFが本質的にラプラス変換であるのと基本的に同じ意味です)。
したがって、数値的には、FFTを使用して畳み込みを処理できます。実際、次のように進行します(特性関数には記号を使用しますが、フーリエ変換は自由に考えることができます):
$ \ phi(Y_1 + Y_2 + ... + Y_n)= \ phi(Y_1)\ times \ phi(Y_2)\ times ... \ times \ phi(Y_n)$
$ \ hspace {2cm} = \ phi(Y_1)^ n $
次に、逆変換によって変換し直します。
数値を操作するプログラムでは、通常のアプローチは、pdfを適切に離散化することです(ある程度大きなパワーに) -of-2個;場合によっては$ 2 ^ {8} $から$ 2 ^ {10} $で十分な場合もあれば、$ 2 ^ {16} $以上が必要な場合もあります)、FFTを取得し、 n乗、元に戻します。定数を正しく処理する場合(とにかく逆FFTによって自動的に処理されるはずですが、最後に$ n $ iid確率変数の合計のpdfへの離散近似が得られます。
実際にはこのような操作は、最初から正しく行うのが少し面倒かもしれませんが、実行が非常に高速になる傾向があります。
===
1: Pham-Gia、T。and Turkkan、N。(1994)。ベータコンポーネントの寿命を持つスタンバイシステムの信頼性。信頼性に関するIEEEトランザクション、71–75。