コメントの質問に答えて、cdf法よりも離散分布を行う可能性のある*高速な方法の概要を以下に示します。
*離散ケースによってはうまくいくため、「潜在的に」と言います。実装された逆累積分布関数アプローチは非常に高速です。一般的なケースは、追加のトリックを導入せずに高速化するのは困難です。
質問の例のように4つの異なる結果の場合、逆累積分布関数アプローチ(または実質的に同等のアプローチ)のナイーブバージョンは次のようになります。罰金;ただし、カテゴリが数百(または数千、数百万)ある場合は、少し賢くならずに遅くなる可能性があります(最初のカテゴリが見つかるまで、累積分布関数を順番に検索したくないことは確かです。累積分布関数がランダムユニフォームを超える場合)。それよりも速いアプローチがいくつかあります。
[インデックスを使用して値を見つけるための順次よりも速いアプローチに関連している、以下で言及する最初のいくつかのことを見ることができます。単なる「cdfを使用したよりスマートなバージョン」です。もちろん、「ソートされたファイルの検索」などの関連する問題を解決するための「標準」アプローチを検討すると、シーケンシャルパフォーマンスよりもはるかに高速なメソッドになります。適切な関数を呼び出すことができれば、そのような標準的なアプローチで十分な場合があります。]
とにかく、離散分布から生成するためのいくつかの効率的なアプローチへ。
1 )「テーブルメソッド」。 $ n $ span>カテゴリの $ O(n)$ span>になる代わりに、一度設定すると、「シンプル"(a)のこれのバージョン(ディストリビューションが適切な場合)は $ O(1)$ span>です。
a)単純なアプローチ-有理確率を仮定する(上記のデータ例で実行):
-「1」、4つの「2」、2つの「3」、および3つの「4」を含む10個のセルで配列を設定します。離散一様分布(連続一様分布から簡単に実行可能)を使用してサンプルを作成すると、単純で高速なコードが得られます。
b)より複雑なケース-「良い」確率は必要ありません。 $ 2 ^ k $ span>セルを使用します。そうしないと、使用するセルがそれよりも少なくなります。したがって、たとえば、次のことを考慮してください。
x 0 1 2 3 4 5 6P(X = x)0.4581 0.0032 0.1985 0.3298 0.0022 0.0080 0.0002
(もちろん、10000個のセルを持ち、以前の正確なアプローチを使用することもできますが、これらの確率が不合理である場合はどうでしょうか?)
$ k = 8 $を使用しましょう span>。確率に $ 2 ^ k $ span>を掛け、切り捨てて、必要な各セルタイプの数を調べます。
x 0 1 2 3 4 5 6 TotP(X = x)0.4581 0.0032 0.1985 0.3298 0.0022 0.0080 0.0002 1.0000 [256p(x)] 117 0 50 84 0 2 0 253
次に、最後の3つのセルは基本的に「代わりに、この他の分布から生成する」(つまり、p(x)-\ frac {\ lfloor 256 p(x)\ rfloor} {256}をpmfに正規化):
x * 0 1 2 3 4 5 6 TotP(X = x *)0.091200 0.273067 0.272000 0.142933 0.187733 0.016000 0.017067 1.000000
「波及効果」テーブルは、任意の合理的な方法で実行できます(ここに到達する時間は、約1%であり、それほど高速である必要はありません)。したがって、 $ \ frac {253} {256} $ span>の時間のランダムユニフォームを生成し、最初の8ビットを使用してランダムセルを選択し、次の値を出力します。セル;初期設定後、これらすべてを非常に高速に行うことができます。 「2番目のテーブルから生成」というセルにヒットしたときのもう1つの $ \ frac {3} {256} $ span>。ほとんどの場合、 $(0,1)$ span>で単一のユニフォームを生成し、乗算、切り捨て、および配列要素へのアクセスのコストから離散乱数を取得します。
2)「ヒストグラムの2乗」法。これは(1)に関連していますが、各セルは、(連続)一様に応じて、実際には 2つの値のいずれかを生成できます。したがって、1からnまでの離散値を生成し、それぞれの中で、そのメイン値と2番目の値のどちらを生成するかを確認します。有界確率変数で動作します。波及効果テーブルはなく、通常、方法(1)よりもはるかに小さいテーブルを使用します。通常、1:nを選択すると、一様乱数の最初の数ビットが使用されるように設定され、残りの部分は、そのビンの2つの値のどちらを出力するかを示します。
メソッドの概要を説明する最も簡単な方法は、上記の例でそれを行うことです。
分布を4つのビンを持つヒストグラムと考えてください:
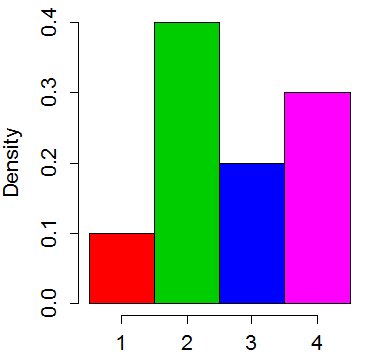
最も高いバーの上部を切り取り、短いバーに配置して、「二乗」します。バーの平均「高さ」は0.25になります。したがって、2番目のバーを0.15カットして最初のバーに配置し、0.05を4番目のバーからカットして3番目のバーに配置します。
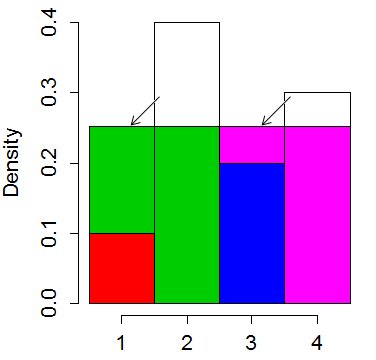
これを1つの色が複数のビンになる可能性がありますが、ビンが2色を超えることはありません。
ここで、4つのビンの1つをランダムに選択します(ユニフォームの上から2つのランダムビットが必要です)。次に、残りのビットを使用して、均一に分散された垂直位置を指定し、色間の区切りと比較して、2つの値のどちらを出力するかを決定します。非常に高速ですが、通常は「テーブル」メソッドほど高速ではありません。
-
これらのメソッドは、無制限の変数を処理するように適合させることができますが、ここでも、ほとんどの場合高速です。 '。
参照: http://www.jstatsoft.org/v11/i03/paper
これらの比較的遅い部分は、値の表;何を生成するかがわかっている場合(「将来、この分布から値を何度もサンプリングする必要がある」)、作成しようとするよりも適しています。 「このASAPから100万の値をサンプリングする必要がありますが、再度実行する必要はありません」と、さまざまな優先順位が作成されます。多くの場合、ソートされた値を検索するための「標準的なコンピューティングアプローチ」(つまり、cdfメソッドをより迅速に実行するため)のいくつかは、実際には最善の選択である可能性があります。
他にも高速なアプローチがあります離散分布からの生成に。注意深くコーディングすれば、非常に高速な生成を行うことができます。例:
3)棄却法(「棄却-棄却」)は、離散分布を使用して実行できます。すでに高速な方法で生成できるスケールアップされた離散pmfである離散メジャー化関数(「エンベロープ」)がある場合、それは直接適応し、場合によっては非常に高速になる可能性があります。より一般的には、連続分布から生成できることを利用できます(たとえば、結果を離散化して離散エンベロープに戻すことにより)。
ここで、便利な累積分布関数(または逆累積分布関数)がない離散確率関数 $ f $ span>があると想像してください- -実際、この図では正規化定数すら持っていなかったため、プロットは正規化されていません:
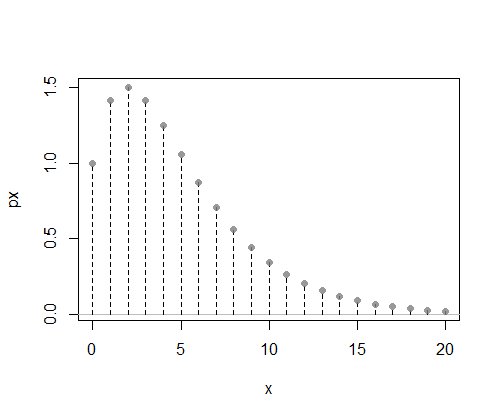
次に、離散確率関数 $ g $ span>から生成するのに便利な関数を見つける必要があります。これには定数 $ c $ span>であり、少なくとも $ f $ span>と同じ大きさである必要があります(これがすべての $ x $ span>値)。つまり、すべての可能な $ x $ span>に対して $ cg(x)\ geq f(x)$ span>です。値。
適切な $ g $ span>を簡単に特定できる場合もありますが、1つの便利なオプションは、左側の部分に離散一様分布を混合することです。右側の $ f $ span>と少なくとも同じくらい重いテールを持つ分布。そのための2つの合理的に便利な選択肢は、幾何分布(テールが指数関数よりもゆっくりと減少していない場合)と、 $ \を取ることによって得られる離散化パレートまたは離散化ハーフコーシー分布のようなものです。一部のパレートまたは半コーシーランダム変量 $ X $ span>のlfloorX \ rfloor $ span>(いずれの場合も、pmfが指数関数的よりもゆっくりと減少している場合)。
(さらに言えば、幾何学自体は指数を離散化することで生成できます。)
この場合、左側の離散一様分布と右側の幾何学が非常にうまく機能します。 :
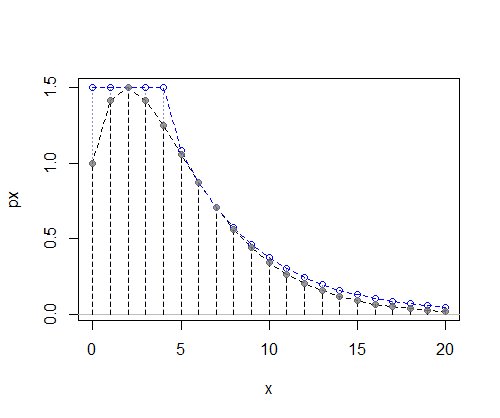
(注意:ここにプロットされているのは正規化されていないpmfであるため、y軸は確率を表すのではなく、比例するものを表します。確率に)
次に、手順は、 $ g $ span>から提案された値 $ x $ span>をシミュレートすることです。 $(0、cg(x))$ span>で $ U $ span>をシミュレートし、 $ U<f $ span>、提案された $ x $ span>を受け入れます(それ以外の場合は拒否し、新しく提案された $ x $ span>)。